1.推荐系统中的多样性
推荐给用户的物品两两间不相识,则说明推荐有多样性。
1.1 物品相似性的度量
基于物品属性标签:类目、品牌、关键词......
基于物品向量表征:
- 用召回的双塔模型学到的物品向量,不适用于多样性问题(不好)
- 基于内容的向量表征(好)(用CV和NLP提取内容特征)
(1)基于物品属性标签
- 物品属性标签:类目、品牌、关键词......
- 标签通常是通过 CV 或 NLP 算法通过图文推算的,不一定准确
- 根据 一级类目、二级类目、品牌 计算相似度
- 物品 i :美妆、彩妆、香奈儿
- 物品 j :美妆、香水、香奈儿
- 相似度:, ,,意思是一级类目相同,二级类目不同,三级类目相同;
- 对三个相似度求加权和,其中的权重根据经验来设置
(2)基于向量表征计算相似度
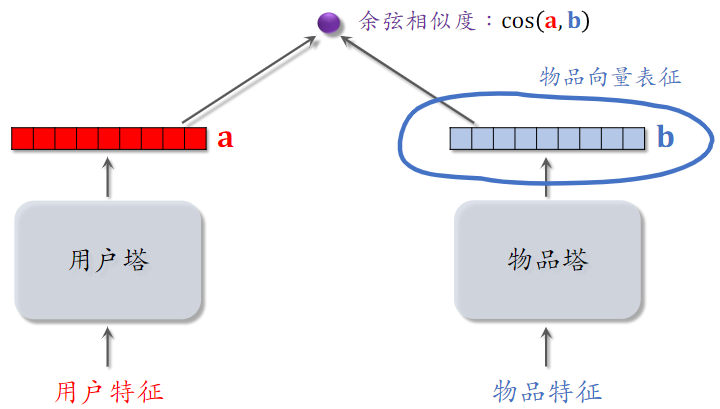
下图为双塔模型,两个向量的余弦相似度记为用户兴趣;
在多样性问题上,我们只需要物品塔的输出;如果两个向量相似,这物品向量表征的内积比较大;
如果把双塔学到的特征用在多样性问题上,也可以用,但是效果不太好。原因是推荐系统的头部效应明显,新物品 和 长尾物品 的曝光少,双塔模型学不好 新物品 和 长尾物品 的向量表征。
(3)基于图文内容的物品表征
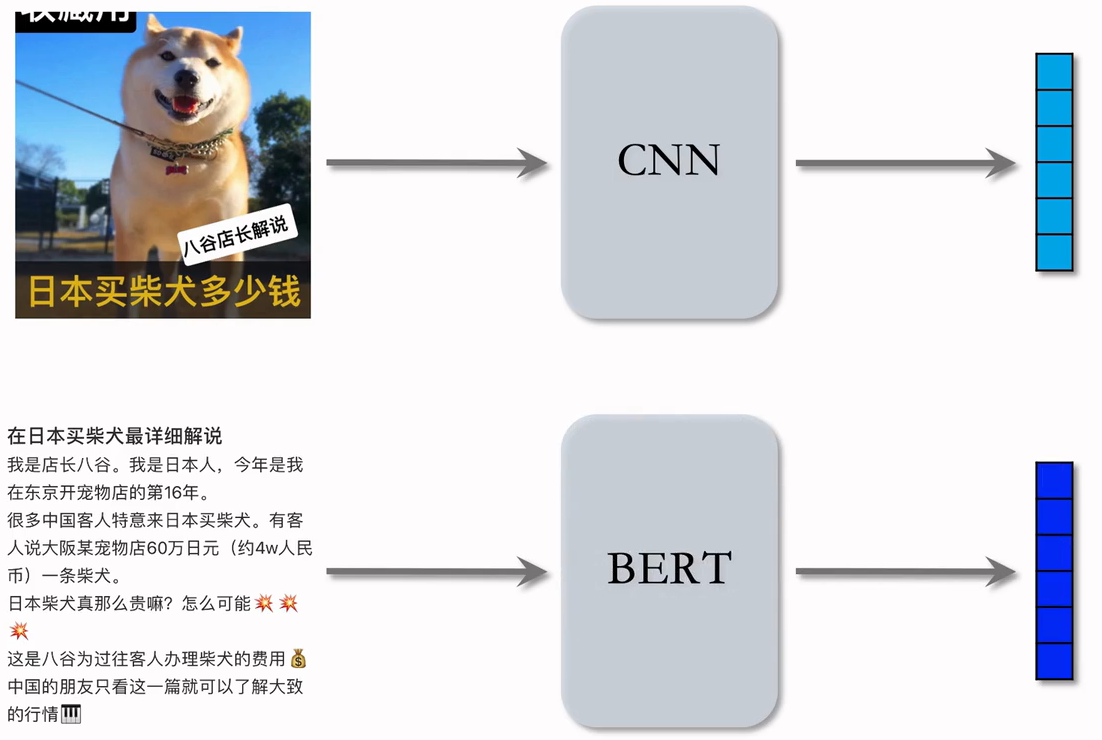
- CNN提取图片特征,BERT提取文字特征,把这两个向量拼起来,就是一篇笔记的向量表征。但是,该如何训练CNN个BERT?
- CLIP[1] 是当前公认最有效的预训练方法
- 思想: 对于 图片—文本 二元组,预测图文是否匹配
- 优势:无需人工标注。小红书的笔记天然包含图片 + 文字,大部分笔记图文相关
- 做预训练时:同一篇笔记的 图文 作为正样本,它们的向量应该高度相似;来自不同笔记的图文作为负样本(Batch内负样本)。
- 参考文献:Radford et al. Learning transferable visual models from natural language supervision. In ICML, 2021.
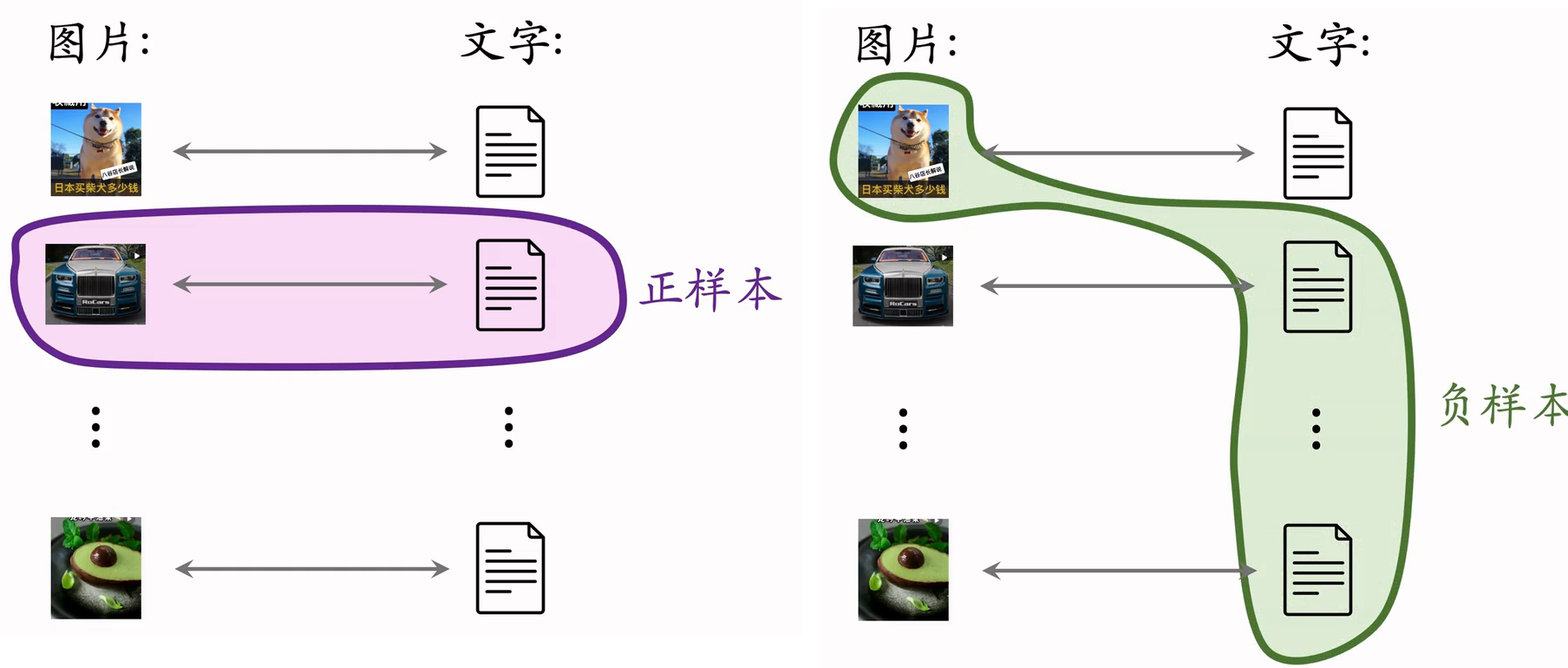
- 一个 batch 内有 m对正样本;
- 一张图片和 和m-1条文本组成负样本;
- 这个 batch 内一共有 m(m-1) 对负样本
1.2 提升多样性的方法
(1)粗排和精排

- 粗排和精排用多目标模型对物品做 pointwise 打分,把每个物品作为独立的个体,准确预估交互、时长等。只考虑打分,而不考虑物品间的关联。
- 对于物品i,模型输出点击率、交互率的预估,融合分数
- 表示用户对物品i的兴趣,在排序中就是物品本身的价值。
(2)后处理
后处理的主要目的就是多样性
给定n个候选物品,排序模型打分,...,reward_n;
从n个候选物品种选出k个,既要他们的总分高,也需要他们有多样性。

- 精排的后处理通常被称为 —— 重排,决定了那k个物品获得曝光;促排之后的多样性也是挺重要的,能显著提高指标。
- 增加多样性可以显著提升推荐系统指标(尤其是时长、留存率)
2.Maximal Marginal Relevance (MMR)
2.1 多样性
- 多样性给n个候选物品打分,融合之后的分数为 , ...,
- 把第i和j个物品的相似度记作,他可以是使用相似度计算或是向量表征计算得出。
- 从n个物品中选出k个,既要有高精排分数,也要有多样性。即结合reward和sim这两种分数,从n个物品中选出k个作为曝光的结果。
2.2 MMR 多样性算法

给未选中的物品打分:计算集合中每个物品的Marginal Relevance分数:

- 是已选中的物品,是未选中的物品
- :衡量j于集合s的相似度,如果相似,则这一项较大
- :介于0~1之间的参数,平衡价值和多样性
Maximal Marginal Relevance (MMR):

对于所有未选中物品i,计算MR分数,并选出分数最高的物品,把这个物品从集合R移到集合S。
MMR算法小结
- 已选中的物品初始化为空集,未选中的物品初始化为全集
- 选择精排分数最高的物品,从集合移动到中;
- 做轮循环:(每次移动一个,重新算MMR分数)
- 计算集合中所有物品的的分数
- 选出分数最高的物品,将其从移动到。
2.3 滑动窗口
MMR:从物品集合中选出综合精排分数和多样性的物品
以这样的方式计算MMR,但存在一个缺点:
- 已选中的物品越多(集合越大),越难找出物品 ,使得与中的物品都不相似。
- 设sim的取值范围是。当S很大时,多样性分数 总是等于1,导致MMR算法失效。
解决方案:设置一个滑动窗口,比如最近选中的10个物品,用代替MMR公式中的。

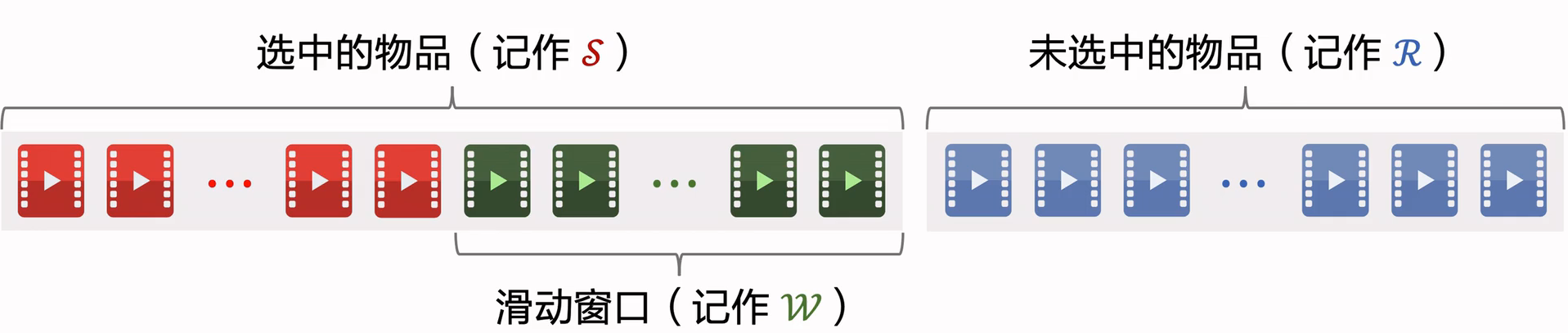
用滑动窗口的可解释性:给用户曝光的连续物品应该不相似,但没必要最新的物品和 30 个之前的物品还不相似
2.4小结
- MMR 使用在精排的后处理(重排)阶段
- 根据精排分数和多样性分数给候选物品排序
- MMR 决定了物品的最终曝光顺序
- 实际应用中通常带滑动窗口,这样比标准 MMR 效果更好
3.重排的规则
- 工业界的推荐系统一般有很多业务规则,这些规则通常是为了保护用户体验,做重排时这些规则必须被满足
- 下面举例重排中的部分规则,以及这些规则与 MMR 相结合
- 规则的优先级高于多样性算法
3.1重排的规则
(1)规则:最多连续出现 k篇某种笔记
- 小红书推荐系统的物品分为图文笔记、视频笔记
- 最多连续出现 篇图文笔记,最多连续出现k=5篇视频笔记
- 如果排i到i+4的全都是图文笔记,那么排在i+5的必须是视频笔记。
(2)规则:每k篇笔记最多出现1篇某种笔记
- 运营推广笔记的精排分会乘以大于 1 的系数(boost),帮助笔记获得更多曝光。
- 为了防止 boost 影响体验,限制每篇笔记最多出现1篇运营推广笔记。
- 如果排第1位的是运营推广笔记,那么排i+1到i+8的不能是运营推广笔记。
(3)前t篇笔记最多出现k篇某种笔记
- 排名前t篇笔记最容易被看到,对用户体验最重要(小红书的top4为首屏)
- 小红书推荐系统带有电商卡片的笔记,过多可能会影响体验;
- 前t=1篇笔记最多出现k=0篇带电商卡片的笔记;
- 前t=4篇笔记最多出现k=1篇带电商卡片的笔记。
注:不是小红书的真实数据
3.2 MMR + 重排规则
- MMR 每一轮选出一个物品:

- 重排结合 MMR 与规则,在满足规则的前提下最大化 MR
- 每一轮先用规则排除点中部分物品,得到子集
- MMR公式中的替换成子集,选中的物品符合规则
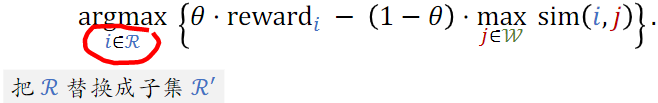
4.DPP:数学基础
- DPP:行列式点过程
- DPP 的目标是从一个集合中选出尽量多样化的物品,契合重排的目标
- 它是目前推荐系统领域公认的最好多样性算法
4.1超平行体示例
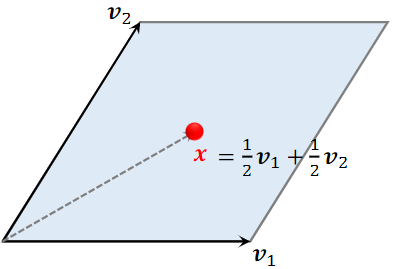
2 维空间的超平行体为平行四边形
- 向量和是平行四边形的两条边,确定一个平行四边形
- 平行四边形中的点可以表示为:
- 系数 和的取值范围是
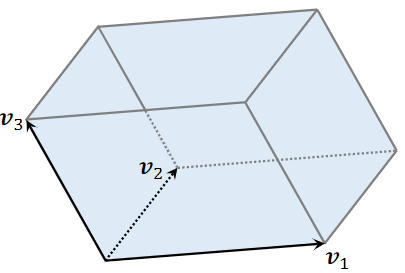
3 维空间的超平行体为平行六面体
- 平行六面体中的点可以表示为:
- 系数 ,,的取值范围是
4.2 超平形体数学定义
一个向量 可以确定一个k维超平形体;这些向量是超平形体的边,都是d维向量。
要求,比如d=3维空间中有k=2维平行四边形。
如果线性相关,则体积。(例:有k=3个向量,落在一个平面上,则平行六面体的体积为0)
4.3 平行四边形的面积
以为底,计算高,两个向量必须正交。
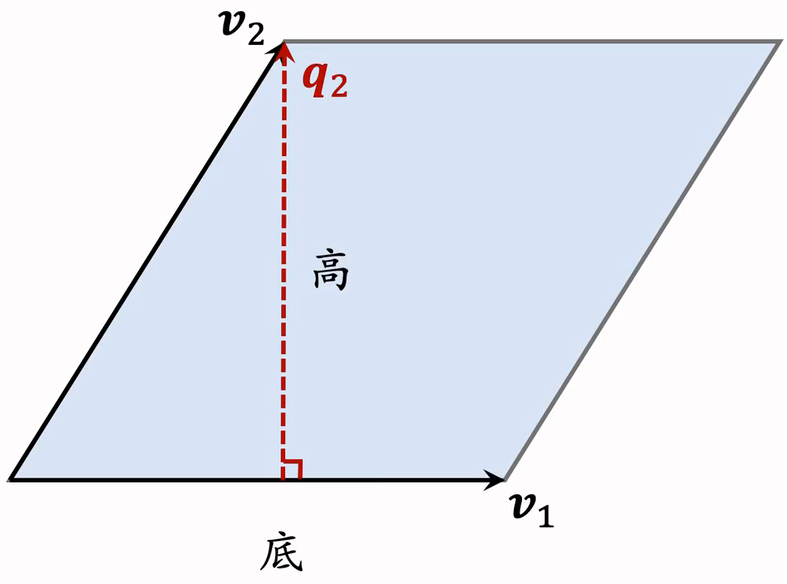
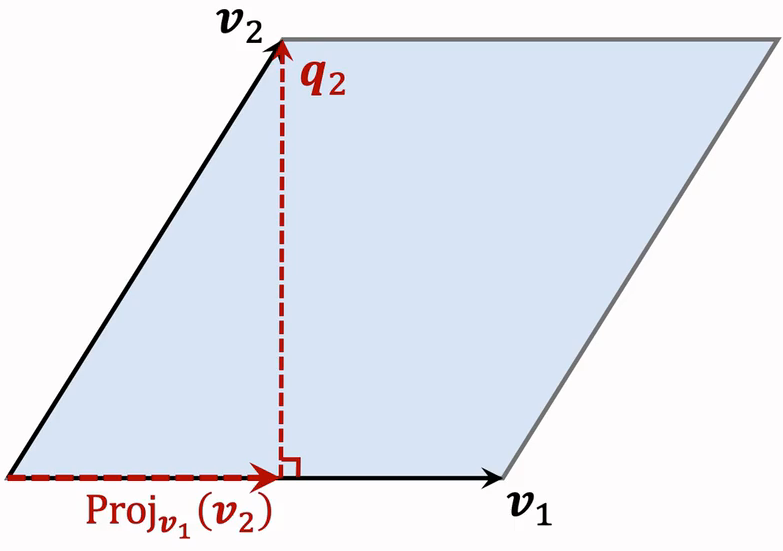
以为底,如何计算高?
- 计算在上的投影:
- 就算
- 性质:低与高正交
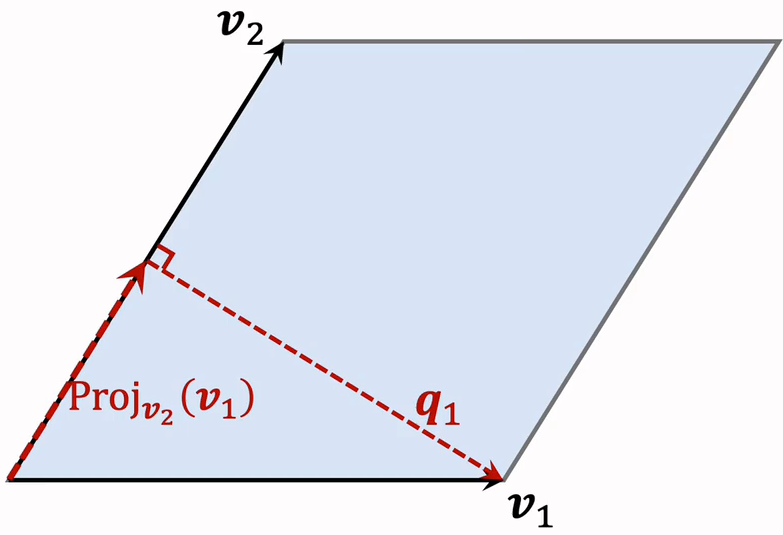
以为底,如何计算高?
- 计算在上的投影:
- 就算
- 性质:低与高正交
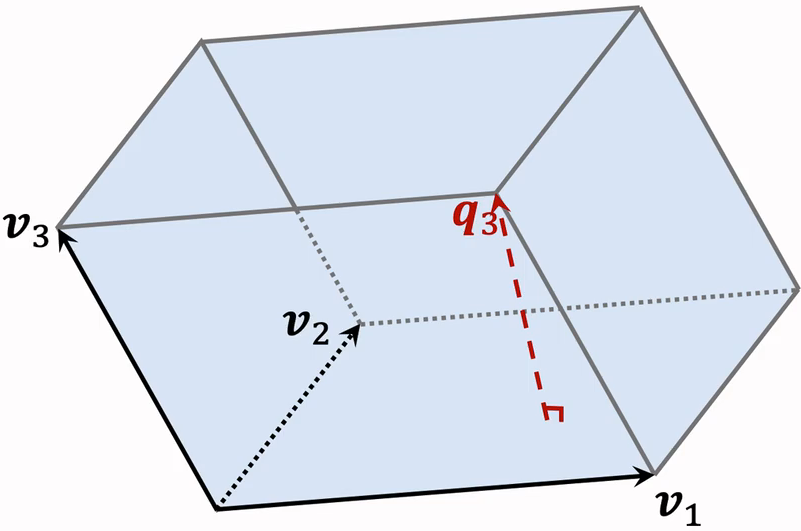
4.4 平行六面体的体积
平行四边形 是平行六面体的底。
高垂直于底
体积何时最大化、最小化?
- 设 , 都是单位向量。
- 当三个向量正交时,平行六面体为正方体,体积最大化,vol=1
- 当三个向量线性相关时,体积最小化,vol=0
4.5衡量物品多样性
(1)体积衡量多样性
给定k个物品,把他们表征为单位向量 。()
用超平行体的体积衡量物品的多样性,体积介于 0 和 1 之间;
如果 两两正交(多样性好),则体积最大化,vol=1
如果 线性相关(多样性差),则体积最大化,vol=0
(2)行列式衡量多样性
给定k个物品,把他们表征为单位向量 。()
把他们作为矩阵的列;
设 ,行列式与体积满足:
因此,可以用行列式 衡量向量 的多样性
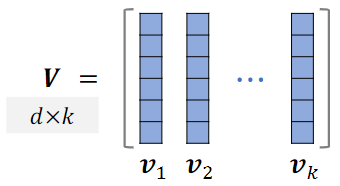
- 行列式和体积是等价的
5.DPP:多样性算法
5.1 多样性问题
精排给n个物品打分:
n个物品的向量表征:
从n个物品中选出k个物品,组成集合
- 价值大:分数之和 越大越好
- 多样性好:S中k个向量组成的超平行体 的体积越大越好
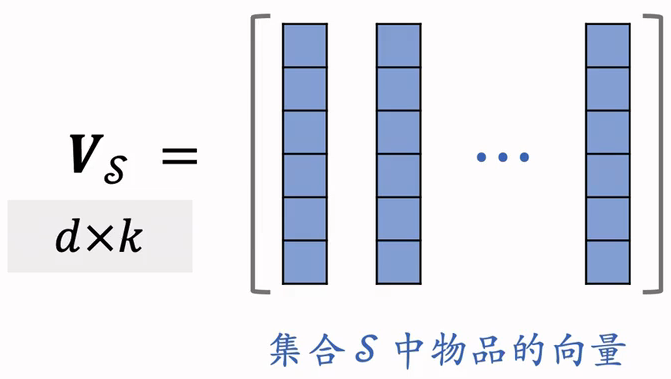
集合S中的k个物品的向量作为列,组成矩阵
以这k个向量作为边,组成超平形体;体积可以衡量S中物品的多样性。
设k≤ d,行列式与体积满足:
5.2 行列式点过程(DPP)
基本思想:使用行列式衡量多样性
DPP 是一种传统的统计机器学习方法:
- 该公式严格来说叫 k-DPP
Hulu 的论文将 DPP 应用在推荐系统:
- 前半部分计算集合中物品的价值,越大表示选中的物品越符合用户的兴趣
- 后半部分是行列式的对数,测量合集S中的多样性;物品多样性越好,这部分越大
- Hulu 论文的主要贡献不是提出该公式,而是快速求解该公式
参考文献:Chen et al. Fast greedy map inference for determinantal point process to improve recommendation diversity. In NIPS, 2018.
5.3 DPP 应用在推荐系统:

- 设A为的矩阵,它的(i,j)元素为
- 给定向量 ,需要的时间计算A
- 为A的一个子矩阵。如果i,则是的一个元素
DPP公式可以等价写成以下形式:
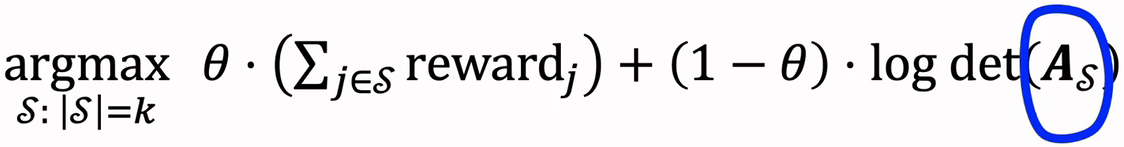
DPP是个组合优化问题,从集合中选出一个大小为k的子集S。
用S表示已选中的物品,用R表示未选中的物品,贪心算法求解:
- :是物品i的价值,希望下一个物品也有较高的价值
- :行列式的对数,括号中是A的一个子矩阵,这个子矩阵比多了一行和一列,行列式会发生变化,我们希望添加的物品i能让行列式尽量大,即物品i和行列式中的物品尽量不相似,否则行列式为0.
5.4 求解 DPP
贪心算法求解:
- 初始时中只有一个物品,是1的矩阵
(1)暴力算法
- 对于单个,计算的行列式需要时间,因为需要对矩阵分解。
- 对于所有的,计算行列式需要时间
- 需要求解上式k次才能选出k个物品。如果暴力计算行列式,那么总时间复杂度为:
- 暴力求解的总时间复杂度为:
- 其中 是计算矩阵的时间复杂度,是计算行列式时间
n的量级是几百,d和k的量级都是几十。这个时间复杂度看起来不大,但系统留给多样新计算的时间只有十几毫秒,复杂度还是有点高。
(2)Hulu的快速算法
Hulu的论文设计了一种数值算法,仅需的时间从n个物品中选出k个物品。
- 给定向量 ,需要的时间计算A
- 用时间计算所有的行列式(利用Cholesky分解)。
Cholesky分解,其中L是下三角矩阵(对角线以上元素全零)
Cholesky分解可供计算的行列式:
- 下三角矩阵的行列式等于对角线元素乘积。
- 的行列式为
给添加一行一列,Cholesky矩阵的变换非常小,能快速算出的行列式。
已知,则可以快速求出所有的Cholesky分解,因此可以快速计算出所有的行列式。
5.5 DPP 的扩展
(1)滑动窗口
用表示已选中的物品,用表示未选中的物品,DPP的贪心算法求解:
DPP缺点:随着集合S增大,其中相似物品越来越多,物品向量会趋近线性相关;行列式会坍缩到零,对数趋于负无穷。
用滑动窗口公式:
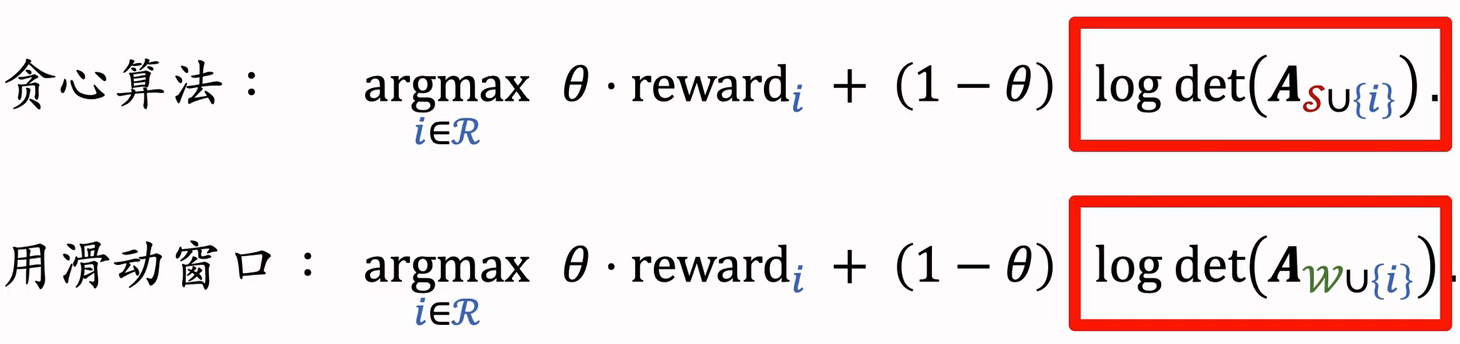
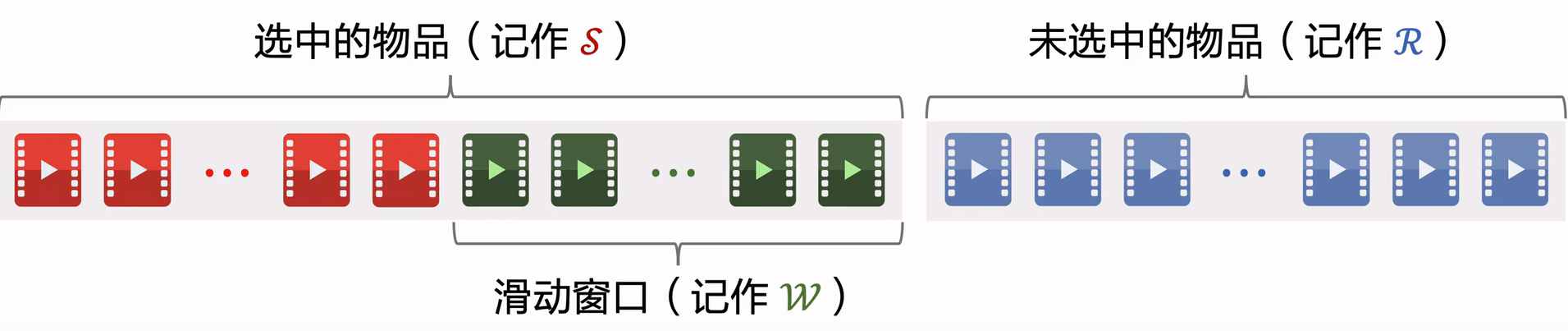
(2)规则约束
贪心算法每轮从R中选出一个物品:
有很多规则约束,例如最多连续出 5 篇视频笔记(如果已经连续出了 5 篇视频笔记,下一篇必须是图文笔记)
用规则排除掉中部分笔记,得到子集,然后求解: